承上文,我们应用简单的Fulop模型对平行平面结进行了分析,对复杂的Chynoweth模型进行了化简,由化简的公式可得碰撞电离率积分和外加电压之间存在一定的关系。
这一关系通常可以用Miller公式[38]表征,即:
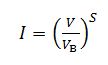 (1)
(1)
其中的I为碰撞电离率积分,V为外加电压,VB为结的击穿电压,S为Miller常数。
在设计器件时,耐压设计是很重要的一环。这关系到耐压区掺杂,厚度等一系列问题。Miller公式可以用于判断开基区晶体管或Shockley二极管的正向阻断电压。Miller公式中S参数与掺杂浓度存在着密切关系。
此次,我们将基于已有的Miller公式,应用MATLAB对不同漂移区掺杂浓度下的S参数进行确定,提出参数S与漂移区掺杂浓度N的拟合公式,并验证其准确性。
此处依然采用MEDICI中的准确的Chynoweth模型对碰撞电离率积分进行提取:
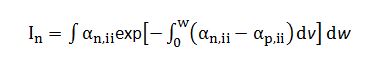 (2)
(2)
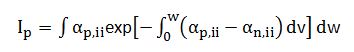 (3)
(3)
由于随着外加电压的增大,an,ii和ap,ii的变化趋势和大小相差很小,假设电子与空穴的碰撞电离率近似相等。
因此碰撞电离积分可表示为:
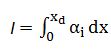
当电压达到雪崩击穿电压时,电流急剧上升,势垒区流出的载流子电流远远大于流进的载流子电流,二者的比值称为雪崩倍增因子,用符号M来表示。
经计算M与碰撞电离率之间关系为:
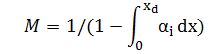
当发生雪崩击穿时,M趋向于无穷大,则I等于1,即碰撞电离率积分等于1时的外加电压就是所谓的雪崩击穿电压VB。此时势垒区对应的最大电场为击穿电场Ec。
可以采用extract语句在MEDICI对碰撞电离率积分进行提取。
在对P+N结构仿真中,先将P区浓度固定为1×1018 cm-3,N区浓度为5×1015cm-3,P区长度设为20μm,N区长度如图1所示保证为非穿通型即可。
然后对PN结施加反向电压VKA,当碰撞电离率积分达到1时,对应的雪崩击穿电压VB为85.2 V。碰撞电离率积分伴随着外加电压的增大而增大。
对于S值,可以将碰撞电离率积分与外加电压在MATLAB中应用I1 = (V/85.2)S进行数据拟合得到为6.118。
为了验证拟合的准确性,将S与VB两个常数带入到3-16中得到I1 = (V/85.2)6.118,分别做出了I1-V曲线图与I2-V曲线图。I1-V是通过拟合得到的Miller公式中碰撞电离率积分与外加电压的关系曲线,I2-V是由MEDICI直接提取出来的碰撞电离率积分与外加电压的关系曲线。
结果下图1所示:
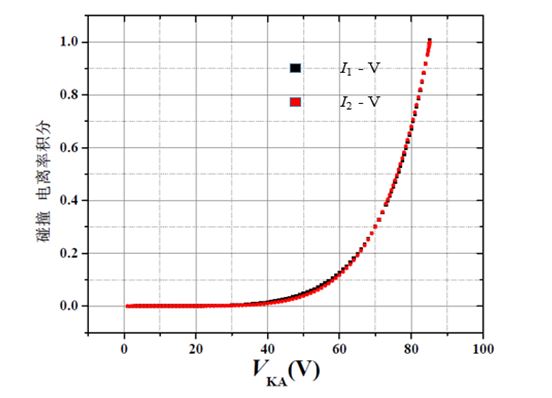
图1 碰撞电离率积分与外加电压的关系图
从图1中可以看出拟合出的碰撞电离率积分与外加电压的关系曲线(红色曲线)与提取出的碰撞电离率积分与外加电压关系曲线图(黑色曲线)几乎完全重合。
经计算,其最大误差为0.23 %,证明了通过这种拟合方法得到的S参数值是可靠的。这一误差可能来自S参数的单一取值,因为S参数会随外加偏压的变化而变化,当电压较小时S比较小,偏压增大时S也增大,所以反向电压接近击穿电压VB时,电流的增长是极为迅速的。
S参数还和掺杂浓度的大小密切相关,虽然上面的拟合方式存在误差,但准确性是可以接受的。为了得到S参数与掺杂浓度的关系式,可以采用相同的仿真方法,P区浓度不变,N区浓度从4×10013 cm-3到9×1015 cm-3依次增大,得到在不同N区掺杂浓度下的雪崩击穿电压VB和对应的S值。
具体结果如表1所示:
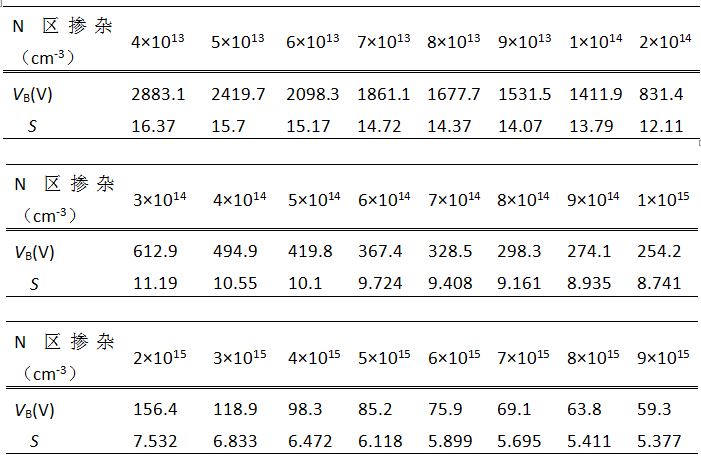
表1.不同浓度下的击穿电压和S值
从表1中可以看出随着N区掺杂浓度的变大,击穿电压和S值逐步下降。
做出S-N关系曲线,推测S参数与掺杂浓度N之间存在幂函数的关系。因此分别采用s=a×Nb和s=a×Nb+c对S-N进行MATLAB拟合。
得到了如下两个关系式:
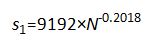 (4)
(4)
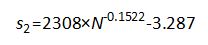 (5)
(5)
对于这两个近似公式的准确性,分别做出S-N, S1-N和S2-N三条曲线。
其中S-N是基于Miller公式提取出来的S与N的关系曲线,S1-N和S2-N是分别采用式4与5得到的S与N的关系曲线,如图2所示。从图2中可以看出上面两式拟合出的曲线与真实曲线基本重合,经计算4式的最大误差0.25%,5式的最大误差为0.18 %。
因此可以根据掺杂情况,应用这两个拟合公式,确定S参数的大小,再应用Miller公式进一步明确外加电压与碰撞电离率之间的关系。
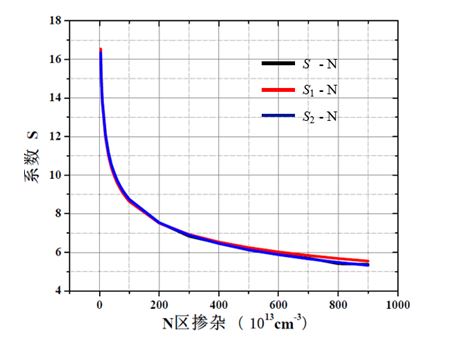
图2 拟合曲线与真实曲线的比较
不同掺杂浓度下的S和VB的确定还可以用于计算开基区晶体管的正向阻断电压。
由于开基区晶体管击穿条件为αM = 1,因此
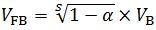
其中S和VB可以根据浓度应用拟合公式得到,α的定量计算超出本文的讨论范围。因此VFB就可以计算出来。
本文阐述了雪崩击穿电压与轻掺杂区浓度变化的关系,对碰撞电离率积分与外加偏压的关系和Miller公式中S参数与轻掺杂区浓度的关系应用MATLAB进行了拟合,得到了近似的I-V表达式,S-N表达式,并对这些表达式进行了准确性的验证。
这种关系的确定,对分析开基区晶体管或晶闸管(如Shockley二极管)的正向阻断电压时有一定的借鉴意义。
*博客内容为网友个人发布,仅代表博主个人观点,如有侵权请联系工作人员删除。