前面论述了电荷在半导体中的运动机制，即电流。

那么半导体中的电荷从何而来，又到哪里去呢？

我们可以将其理解为某个特定部落的人口问题，在这个部落，人口统计只计算单身人口，夫妻不计入统计范围内。某天突然多出了几个人，那么这几个人的来历只可能有两种，一是外来人口（假设都是单身），二是内部降生新生儿。同理于电荷：要么由外部流入，要么由内部产生。

那么电荷的归宿也只有两种，要么内部复合消失（成为夫妻，不计入统计范围），要么流出到外部（外出）。我们用下图模型表示。

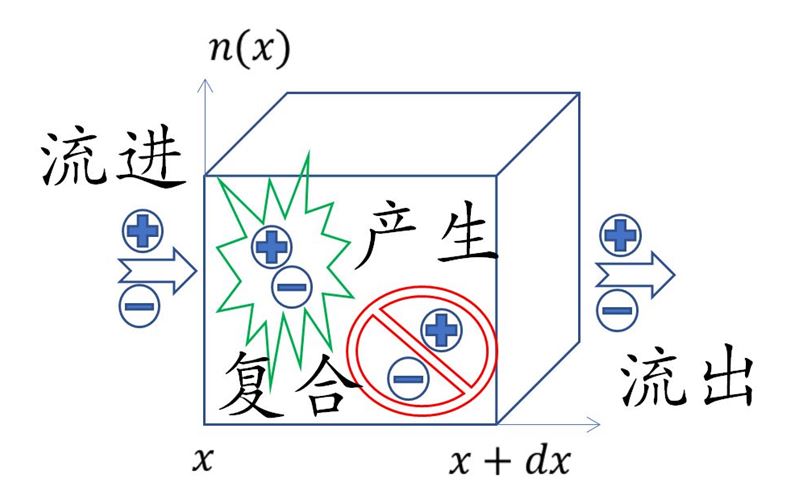
➤暂不考虑其他因素计算电荷变化率。

电荷变化率能帮助我们了解特定空间内电荷的产生和消失状况。电荷（以电子为例）的流入和流出就是电流，那么电流在一维X方向所引起的电荷变化率为：

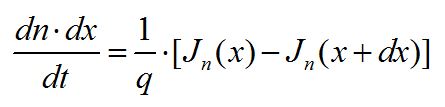
其中，dn∙dx为在dx范围内的电荷变化，单位时间的电荷变化为电荷变化率。

J_n(x)为流入电流，J_n(x+dx)为流出电流。电流密度的定义是单位时间通过单位面积的电荷总量，所以电流密度除以电荷单位就是单位时间内变化的电荷数量。

对于绝对理想的半导体模型而言，上式是成立的（即仅计算外部流入人口和流出人口），但实际上半导体内部因为本征激发会自发地产生自有电荷（新生儿的诞生），同时因为材料中的杂质、缺陷等，自由电荷也会有寿命，即“复合”（联姻），所以上述公式并不能用于表征实际半导体内部的电荷变化情况。

既然出现了不确定因素，那我们就需要搞清楚这个不确定因素是如何出现的，即电荷为何会自发产生，又为何为自发复合。

➤首先来看为什么会电荷会自发地产生。

若要严谨地推导电荷产生的过程，需要固体物理和量子力学的基本知识，严格求解薛定谔方程，过程会比较晦涩，教科书上都能找到详细推导过程。但若完全脱离这些基础，又难以讲清来龙去脉。这里尝试将其、中比较关键的物理概念以及他们的逻辑关系提炼出来，以便读者理解。

基本逻辑是：自由空间的电子→周期空间的电子→能带（导带&价带）→费米分布→电子态密度→电子浓度，此次先讲自由空间的电子和周期空间的电子。

首先，微观粒子具有波粒二象性，这是大家熟知的，因此电子的运动状态可以用波函数来表示。

我们想象在一维空间中（只有x方向）有两种处于不同环境的电子，一是处于自由空间的电子，传输过程中没有任何边界；二是处于周期排布空间的电子（晶体材料的原子都是周期排布）。

由于测不准原理（位置和速度不能同时为确定值），两种环境中的电子在某个x位置只能以存在概率来表达，那么自由空间和周期排布空间的电子的存在概率分别如何呢？

①对于自由空间中的电子，其电子波函数表达式为：

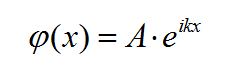
其中，，物理名称为“波矢”，也就是代表了电子波函数的传播方向，λ为电子波函数的波长。

用以表示电子出现在x位置的概率，

,A为振幅。对于自由空间的电子波函数，A为常数，所以电子在自由空间中各个位置出现的概率相同，也就是说电子在自由空间可以自由运动。

②对于处于周期排布空间的电子，假设周期为a, a_n=n∙a,那么其波函数也相应为周期性，可表达为：

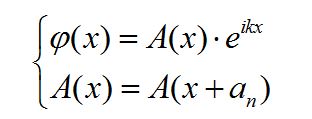
注意，电子在每个周期a内的波函数受调制，而A(x)不是常数，所以电子在一个周期内各位置出现的概率不同，但电子在不同周期之间的相对位置却是重复的。

将x=x+a_n带入，我们发现周期性电子波函数成立的必要条件是。

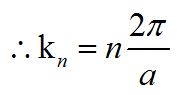
对比自由空间电荷的波矢k和周期性空间的波矢k_n，可以发现，周期性空间导致波矢出现了离散化。（需要注意的是，两种空间的波矢k物理意义有所不同，前者表示的单个电子波函数，而后者描述的是一个周期内的波函数）。

由于k的离散化，电子的能量随k的变化也会发生离散化。量子力学对微观粒子的能量表达式为：

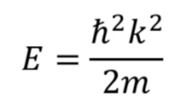
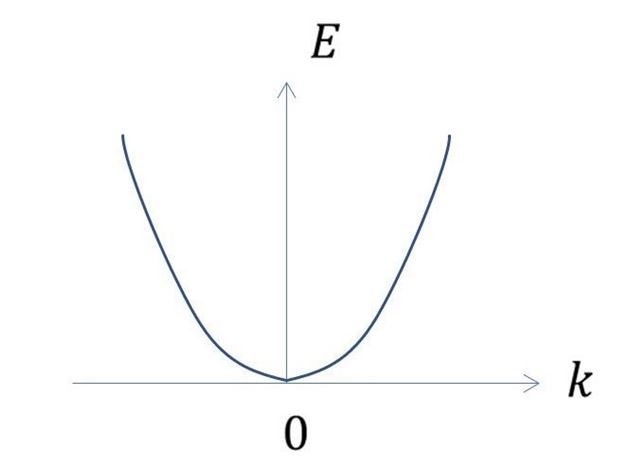
其中，h为普朗克常数。（将ϕ（x）表达式代入薛定谔方程就可得出，在此不做赘述）。因此自由电子能量E与波矢k成抛物线关系，是连续分布的，如下图所示。

而将抛物线的k坐标离散化k_n，就会将连续E曲线离散为能级，且能级在每个周期内聚集，周期交接处会出现间隙，如下图所示。

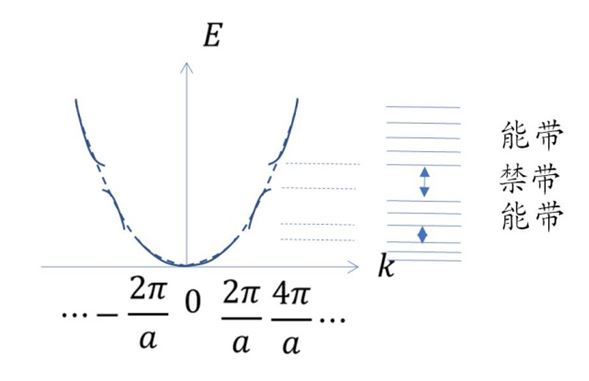
半导体物理中就将聚集的能级称为能带，即电子可以存在的地方；而周期交接处的间隙称为禁带，即电子不能存在的地方。

文末总结

1.理想状态下电流在一维X方向所引起的电荷变化率：

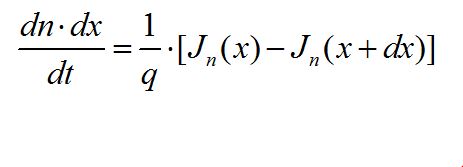
2.非理想状态下，存在电荷自发产生和自发复合的现象，因此提出“电荷为何会自发产生”的问题。

3.解答问题的第一步：分析自由空间和周期排布空间的电子的存在概率。

4.得到结论：自由空间中电子在各个位置出现的概率相同；周期排布空间中电子在一个周期内各位置出现的概率不同，但在不同周期之间的相对位置相同。

5.通过对比自由空间电荷的波矢k和周期性空间的波矢k_n，发现周期空间内电子的能量随k的变化发生离散化，进而引出能带和禁带的基本概念。

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。