一、电流与速度

了解完电场作用下的漂移电流，接下来我们讲解热运动导致的扩散电流。

热运动的最小自由空间为一个平均自由程，即一个粒子通过热运动与相邻粒子相碰撞的平均距离。假设在温度T下，半导体中电子的平均自由程为l，热运动平均速度为v_th，热运动通过一个平均自由程所需时间为。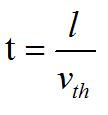

在一维情况下，假设沿x方向的电子浓度分布为n(x)。如图所示“0”点所示位置，其距离最近的邻近电子分别位于l和-l处，相应的电子浓度分别表示为n(l)和n(-l)。根据平均自由程的定义不难理解，最先可能扩散到“0”位置的电子就处于这两个位置。

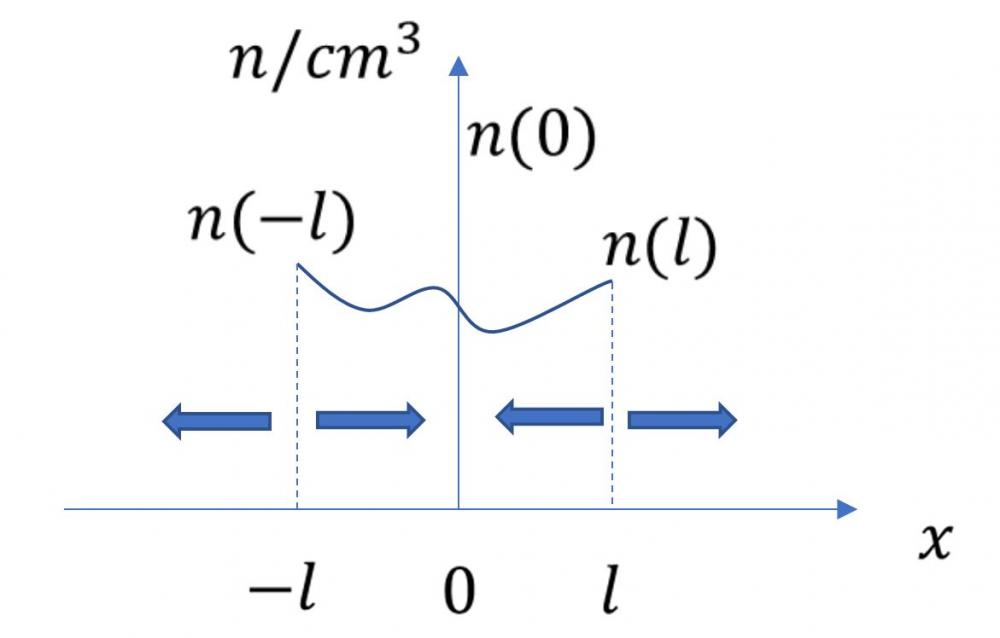
根据电流密度定义，要获知“0”点的电流，就要计算左右两侧n(l)和n(-l)分别在t时间内通过“0”点的电荷总量。

以-l位置的n(-l)个电子为例，在一维状况下，这些电子热运动往左或者往右的概率相同，均为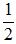。所以，在单位时间内通过“0”点的电荷数量为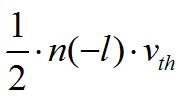，相应产生电流为：

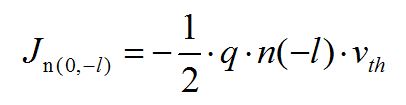
（设电流以x方向为正，添加“-”的原因是电子电流方向与运动方向相反）同理，对于l位置的n(l)个电子在“0”点产生的电流为：

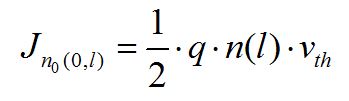
n(l) 和n(-l)在“0”点产生的总电流为：

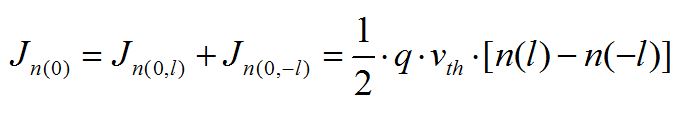
这样，我们就能得到电流J与速度v之间的关系。

二、电流、速度和浓度梯度

进一步地，我们想要梳理清楚电流、速度和浓度梯度之间的关系。

一维浓度梯度的表达方式为浓度n(x)在x方向上的微分，即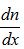。根据J_n(0)的表达式，只需梳理[n(l)-n(-l)]与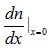之间的关系。

这里可以用到Taylor展开，简单解释如下（想直接看推导结果的伙伴可以跳到结果）：

如果一个函数f(x)在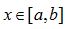区间具有n阶导数fⁿ(x)，且已知在点的值f(x₀)，那么f(x)可以展开为多项式之和：

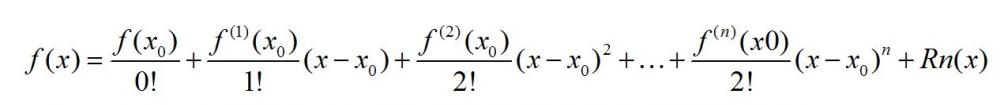其中，Rn(x)是余项，即误差项，是(x-x₀)ⁿ的高阶无穷小。具体推导这里不做赘述，简言之就是可以将任一可求导的函数展开为一个多项式之和，基本规律是x距离x₀越近，那么可取的多项式指数也可以越小，误差也越小（极限情况就是取x=x₀,上式就变成f(x)f(x₀)。

回到扩散电流的推导，因为平均自由程显然是一个微小量（通常为数埃到数百埃，显然半导体中杂质、缺陷越小，平均自由程越大），利用Taylor展开式，可以将n(l)在x=0处展开为：

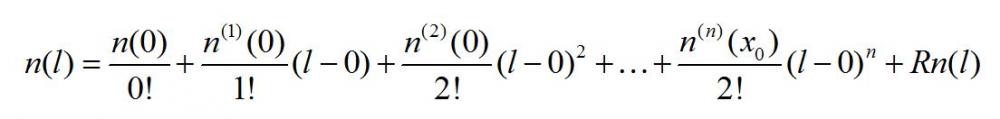在假设l是一个足够小的量的情况下，忽略上式中二次方及以上的多项表达式以及误差项，近似得到：

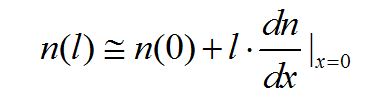
同理：

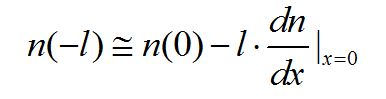
由此我们得到[n(l)-n(-l)]与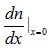之间的关系。

结合前面的电流密度推结论，从而得到：

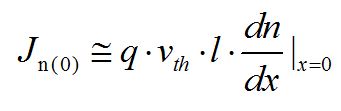
扩展到所有x，有：

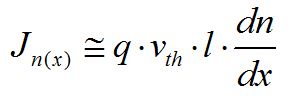
定义电子扩散系数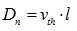，就得到大家常见的电子扩散电流方程：

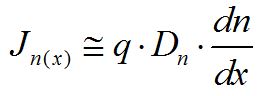
同理，可得到空穴扩散电流方程：

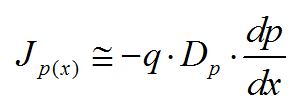
从而，扩散总电流为：

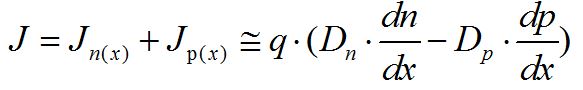
注意：

1.此处在扩散电流的表达式中采用了“约等于”的符号，而绝大多数文献中是直接为等号。从推导过程中，大家容易发现Taylor展开中是作了近似处理。需要知道的是：当半导体晶体质量越高、掺杂浓度越低，这个表达式的精确度也就越差，就需要引入更高阶的多项式来减小误差。

2.扩散电流中的速度是V_th一个统计值，也就是说与漂移电流不同的是，扩散电流等式不适用于单个电荷等不具有统计意义的对象。

至此，我们已分别推导得到漂移电流和扩散电流的表达式，那么半导体中的电荷移动所产生的总电流即为两者之和，即：

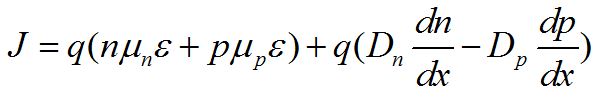
请注意，自此之后，对于上式的使用，我们不再采用“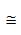”，也就是默认平均自由程足够小，Taylor展开的一阶表达式精度已经足够。

其中，， 分别为电子和空穴在电场作用下的漂移速度；，分别为电子和空穴在存在浓度梯度情况下的扩散速度。

由此，我们达到了本章开篇所述之目的——“梳理清楚了速度与浓度梯度以及电场的关系，自然也就梳理楚了扩散运动以及漂移运动分别形成的电流，而两者之和就是总的电流”。

文末总结

1、在一维情况下，电流J与速度v之间的关系：

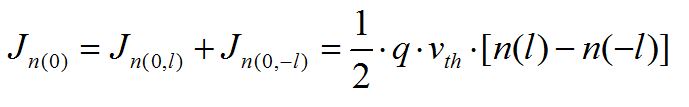
2、电流J、速v和浓度梯度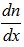之间的关系：

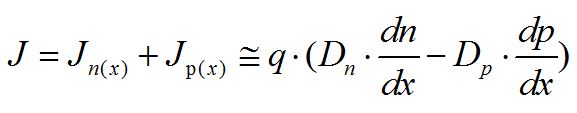
3、半导体中的电荷移动所产生的总电流：

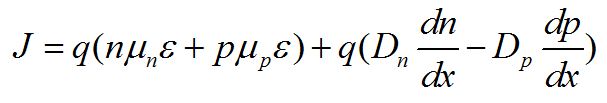
*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。